数  学 

 姓名          分数            

【注意】本测试包括三道大题，时间60分钟，满分150分。测试结束后考卷需还给测试老师，学生不能带走。

 

一、 填空题I：（6分×7=42分）

 

 3、[A，B]=135，（A，B）=27，求A+B=__________.

 4、数列1，4，10，19，31，46……，第10项=__________，第n项=__________

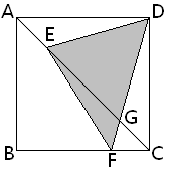
 5、正方形ABCD，边长为8，AE=1/4 AC，CF=1/4 BC，求阴影DEF的面积=__________

 

 

 6、已知2012被一些正整数去除，得到的余数为10，则这样的正整数共有____________个。

 7、 有一组连续的三个正整数，从小到大依次排列，第一个数是5的倍数；第二个数是7的倍数；第三个数是9的倍数；则这组数中最小的正整数为__________。

二、 填空题II；（第11小题12分，其余每题8分，共60分）

8、定义新运算*：a*b=ab-a-b，若（3*x）*3=11，则x=_____________。

 

9、甲、乙、丙都在读同一本故事书，书中有100个故事，已知甲读了85个故事，乙读了70个故事，丙读了62个故事，那么甲、乙、丙3人共同读过的故事最少有___________个。

 

10、如果一个多位数等于它的各位数字之和加上各位数字之积，则称这个多位数为幸运数，则：小于1000的幸运数有___________个。

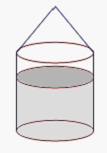
11、一个封闭的容器由一个圆柱体和一个圆锥组成，如图所示，其内放有一些水，圆锥在上的时候水面高度是12厘米，倒放时，水面高度是20厘米，那么这个容器圆锥部分的高是___________厘米。

12、若相同的汉字表示相同的数字，不同的汉字表示不同的数字，则在等式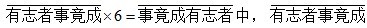：，所表示的六位数是            

13. 有浓度为5%的盐水120克，浓度为7%的盐水300克，浓度为12%的盐水100克混合在一起，得到的混合溶液的浓度为____________。

14. 黑板上写有1,2,3，……，2010,2011这2011个数，我们把“擦掉黑板上的7个数，然后再在黑板写上这7个数的和除以9得到的余数”称为一次操作，经过若干次操作后，黑板上只有一个数，则这个数除以9的余数为____________。

 

三、 解答题（请写出详细解题过程）：（12分×4=48分）

15、甲、乙两件商品，甲商品的成本是250元，乙商品的成本比甲商品低16%，现有以下三种销售方案：

①甲商品按30%的利润率定价，乙商品按40%的利润率来定价；

②甲、乙都以35%的利润率定价；

③甲、乙的定价都是310元。

请问：选择哪种销售方案最赚钱？这时能赢利多少元？

16. 已知a，b，c都是正整数，a，b，c的最大公约数为24，a，b的最小公倍数是360；a，c的最小公倍数是114.

（1）求b的最小值。

（2）若b，c的最小公倍数为240，求a，b，c的值。

17. （1）把1，2，3，……，25这25个数无重复地填入到一个5×5的方格中，使得去掉任意一行与一列后，剩下的16个数的和均为偶数。

（2）实际上，我们不能把1，2，3，……，36这36个数无重复地填入到一个6×6的方格中，使得去掉任意一行与一列后，剩下的25个数的和均为偶数，请你说明理由。

18、（1）请从1，2，3，…，2011中找出1006个数，使得这1006个数中不存在两个数，其中一个是另一个的倍数。

（2）证明：从1，2，3，…，2011中，任意取出1007个数，其中都存在两个数，其中一个是另一个的倍数。