近期,数学建模备受大家关注,人大附、清华附、80中等优质校拔尖培养项目中均已开设数学建模课程;新课改后,数学建模成为新的出题“风向标”;另外,数学建模能促进孩子们数学学习,数学建模优秀作品更能成为助力升学的更有效的证明,提高培养孩子们的创新能力及发现问题,分析问题,解决问题的核心顶级能力,终身受益!为此,北京小升初网整理了历年作品——《羽毛球中的数学》,通过数学建模小论文来感受一下为什么数学建模成为牛娃学习的“热潮”!
数学建模小论文比赛详情+历年作品汇总🔻
数学建模小论文案例-初中:羽毛球中的数学
东北育才外国语初一年级徐同学
摘要:数学无处不在,哪怕在时尚的体育运动羽毛球中也有数学的身影,那么怎样才能在羽毛球比赛中取得高分呢?这篇论文对羽毛球的运行轨迹与球拍击球时倾斜角度和击球力度等问题之间的关系用数学的方法加以讨论研究。论文主要分力度较大的扣杀与力度较小的普通接发球两种情况加以分析。在最后对问题进行了延伸讨论,对在什么情况下球将击界外进行了研究分析。
研究方法:在打羽毛球时,球是以抛物线的路线运行,不过在力度很大时我们可以将球运行的抛物线看作是直线。这时为了讨论球拍角度,球员站位与羽毛球的路线之间的关系,我运用了一些三角函数的知识。然后在击球力度不大时,球以抛物线的轨迹运行,这时羽毛球的运动符合物理中的斜抛运动,我应用了斜抛公式进行探讨。接着为了弄清楚羽毛球飞行的角度我又使用了抛物线的有关知识。在最后讨论羽毛球出界的问题时,为了方便说明球的飞行距离与场地大小之间的比较,我再次运用了三角函数的有关知识。在整篇论文的开始为了讨论球拍角度和羽毛球的飞行方向之间的关系,我用羽毛球拍和羽毛球在家里作了实验,发现他们之间的角度恒为90度。
问题的提出:羽毛球是一种很时尚的体育运动,中国的体育健儿在这一项目的国际赛场上摘金夺银。作为一个羽毛球迷,我很惊叹于运动员们精确的扣杀,精彩的接发球。也很想搞清楚是如何将羽毛球打好的,所以我用数学方法对羽毛球运动的角度、方向、击球的力度等问题进行分析,探寻较佳的击球方式。
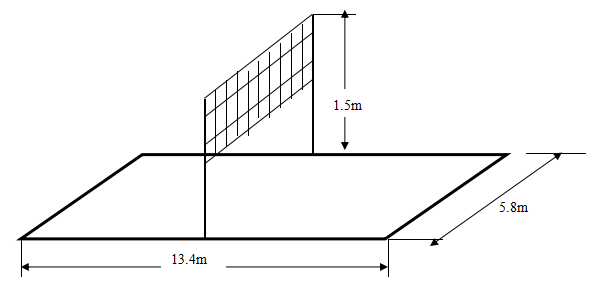
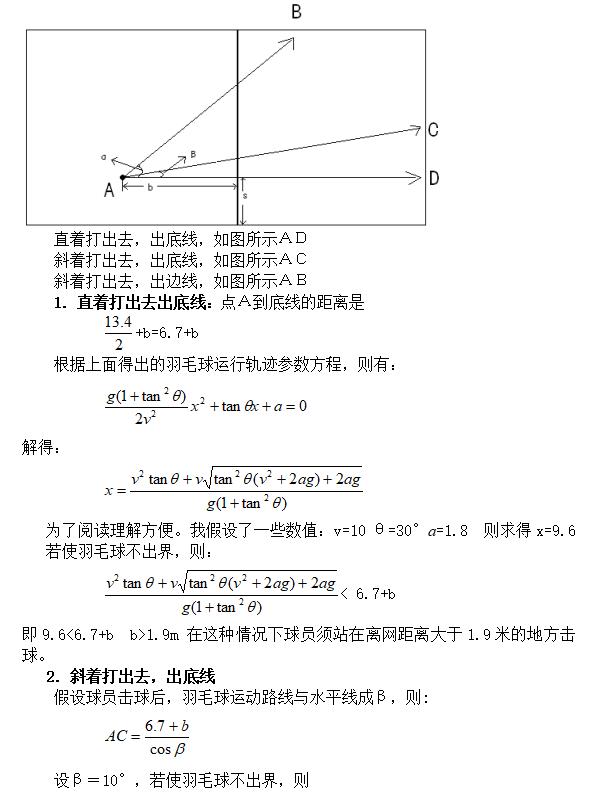
场地说明:网高1.5m,场地长13.4m,场地宽5.8m
假设:以下分析都是在羽毛球不受风力影响的情况下进行的,为了使对方不易接球,假设球员将球击向远离对方球员的位置(例如:如果对方球员在场地左侧,就将球击向场地右侧)
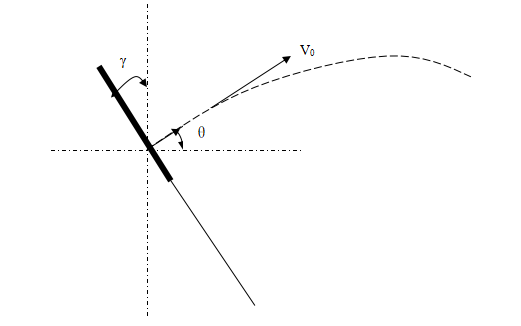
建立模型:我将击球分为两种情况,一种是击球力度较大,击球点较高的“扣杀”;另外一种是击球力度不大,击球点较低的普通击球方式。而且,经过多次实验发现,无论球从哪个角度飞来,被击出后,其初速度及运动方向都与球拍成90°,从下图不难得出结论:羽毛球初速度方向与水平方向角度θ等于球拍与地面垂直方向所成角度γ(击球角度)。
第一种:扣杀
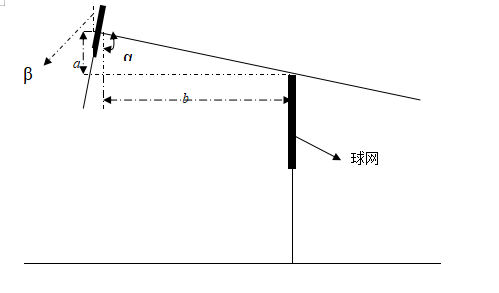
在扣杀的过程中,当球保证过球网时,球的高度越接近球网高度对方越难接到球,也就越精彩,最理想的是“擦网球”。在击球时,球拍倾角越大球员就越容易控制,击球就越容易,反之则越难。如果球员以很大的力度斜向下击球,我们可以将羽毛球的运动轨迹近似看做直线。在下图中,a是球高出球网的高度,b是击球点距球网的水平距离,则有β=90°-α=arctan(b/a)
接着,为了方便讨论a,b与β之间的关系,我代入一些数值:
|
a |
b |
β |
|
1 |
10 |
≈6° |
|
3 |
10 |
≈17° |
|
0.5 |
10 |
≈3° |
|
1 |
12 |
≈5° |
|
1 |
8 |
≈7° |
结论:在水平距离b一定时,接球点越高,球拍越斜,扣球就越容易。在高度一定时,距离越远,球拍越直,扣球越难。
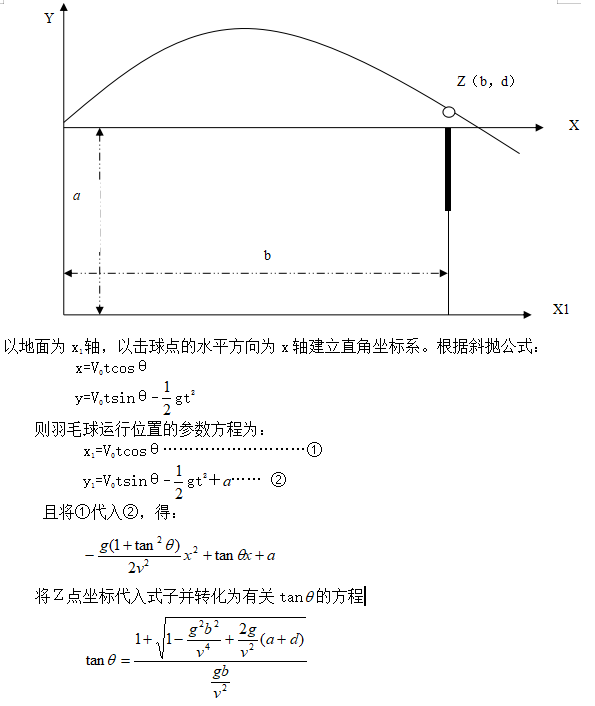
第二种:球以抛物线轨迹运行
如图所示,d是当羽毛球的横坐标是b时的高度,也就是当羽毛球经过球网时时的高度,在比赛中d的值越接近球网高度h越好,但至少要大于h。且球飞得越高,对方就越难判断球的飞行轨迹,接球就越难。若球飞得低,对方接球就越容易。
为了说明θ与v,a,b之间的关系,我又代入了一些数值(暂设d是2m)
|
v |
b |
a |
θ |
|
3 |
2 |
1.7 |
55° |
|
3 |
2 |
2 |
69° |
|
3 |
2 |
1.5 |
54.2° |
|
3 |
3 |
1.7 |
无实根 |
|
3 |
1 |
1.7 |
73.6° |
|
4 |
2 |
1.7 |
67.7° |
|
2.5 |
2 |
1.7 |
38° |
结论:击球点越高,力量越大,球飞得越高,对方就越不容易接到球;而离网越远,球飞得就越低,对方接球就相对容易一些;从这些数值我们还可以看出,羽毛球的初速度的大小必须要大于球员离网水平距离的数值。
问题的延伸 怎样使球不出界
球员击球出界有三种情况:
问题的验证
- 5月15日,“苏迪曼”杯世界羽毛球锦标赛的总决赛在中国和印尼队展开。在第二节中,张军的许多精彩扣球令观众激动不已,通过对其角度的分析,发现其击球角度,羽毛球飞出的角度和他所站的位置正好满足扣球时各角度之间的关系式。
- 在同一场比赛的第三节,张军打了几个将近出边界的球。通过对其击球角度,球速和球员位置之间的关系。得出正好满足击球角度,球速和球员位置之间的不等关系。
体会:随着人们对体育的热爱日渐高涨对其精确的数据需要也越来越强。而我有幸参加了这次竞赛,且对体育运动中较流行的羽毛球的各种问题用数学方法加以分析。在老师的帮助下,通过这次撰写数模论文,我的数学能力有了很大提高,对独立分析问题也有了一定的方法。在写论文的过程中,因为所学知识的限制,遇到了一些困难,曾经想到过放弃,但是想到“都已经做到这了,放弃不是太可惜了嘛”凭着这个信念,我完成了这篇论文。由于能力和时间的关系,论文中难免有这样那样的错误,还望老师们加以指正。
走美数学建模小论文报名了解🔻
👉“走美杯”数学建模小论文常见问题及历年优秀作品集!小升初荣誉ZS汇总!
小升初简历空白?别慌!其他评选、竞赛项目在这里👇小升初这些荣誉ZS千万要提前准备!